FlashAttention：Attention加速

论文链接： FLASHATTENTION: Fast and Memory-Efficient Exact Attention with IO-Awareness

原始 Attention 的实现方式

存储关系

矩阵 $Q, K, V \in R^{N \times d}$ 全部存储在 GPU 的 HBM（High Bandwidth Memory，高带宽显存） 中。

原始 Attention 的计算流程

Q, K, V (词向量序列)
     ↓
S = Q * Kᵀ   →  P = softmax(S)  →  O = P * V

从 HBM 加载 $Q, K$ 到 SRAM（片上缓存）
计算得分矩阵 $S = Q K^{T}$
将 $S$ 写回 HBM
再次从 HBM 加载 $S$ 到 SRAM
计算 Softmax： $P = softmax (S)$
将 $P$ 写回 HBM
从 HBM 加载 $P$ 和 $V$ 到 SRAM
计算输出： $O = P V$
将 $O$ 写回 HBM
返回 $O$

关键问题：显存与访存瓶颈

随序列长度 N 增大，注意力矩阵 S 和 P 的尺寸为 $N \times N$ 。
显存占用与数据传输复杂度为 $O (N^{2})$ 。
每次操作（写回、读取）都需经过高延迟的 HBM，导致：
- 显存爆炸；
- 墙钟时间受限；
- GPU 算力利用率低（memory-bound）。

实际例子

在 Llama3-8B 模型中：

N = 8192（上下文长度）
d = 128（每个 token 的维度） → 注意力矩阵大小为 $8192 \times 8192$ ，即 约 67M 元素，显存开销巨大。

小结

原始 Attention 的主要问题并非算力不足，而是：频繁的 HBM ↔ SRAM 数据传输导致严重的 IO 瓶颈。

FlashAttention 的核心创新，正是重新设计计算流程以减少这些 IO 操作。

Compute-Bound 与 Memory-Bound

Compute-Bound 运算

典型特征：

大规模矩阵乘法
多通道卷积操作这类计算主要受算力限制（compute-bound），即 GPU 的算术单元是瓶颈。

Memory-Bound 运算

典型操作：

按位操作：ReLU、Dropout
规约操作：sum、softmax 这类计算主要受显存访问速度限制（memory-bound），即数据在 HBM 与 SRAM 之间的传输成本成为主要瓶颈。

Memory-Bound 的优化思路

针对 memory-bound 操作，常见优化方法是 fusion 融合算子：

不对中间结果进行显存回写。
在单个 kernel 内完成多步操作，从而减少 HBM 读写次数。

融合可以有效提升效率，但存在限制：

模型训练时必须保留部分中间结果，以便反向传播使用；
因此不能无限制地融合所有操作。

核心优化思路与性能提升

性能对比示意（以 GPT-2 为例）

下图展示了 PyTorch 与 FlashAttention 在 Attention 计算中的耗时对比：

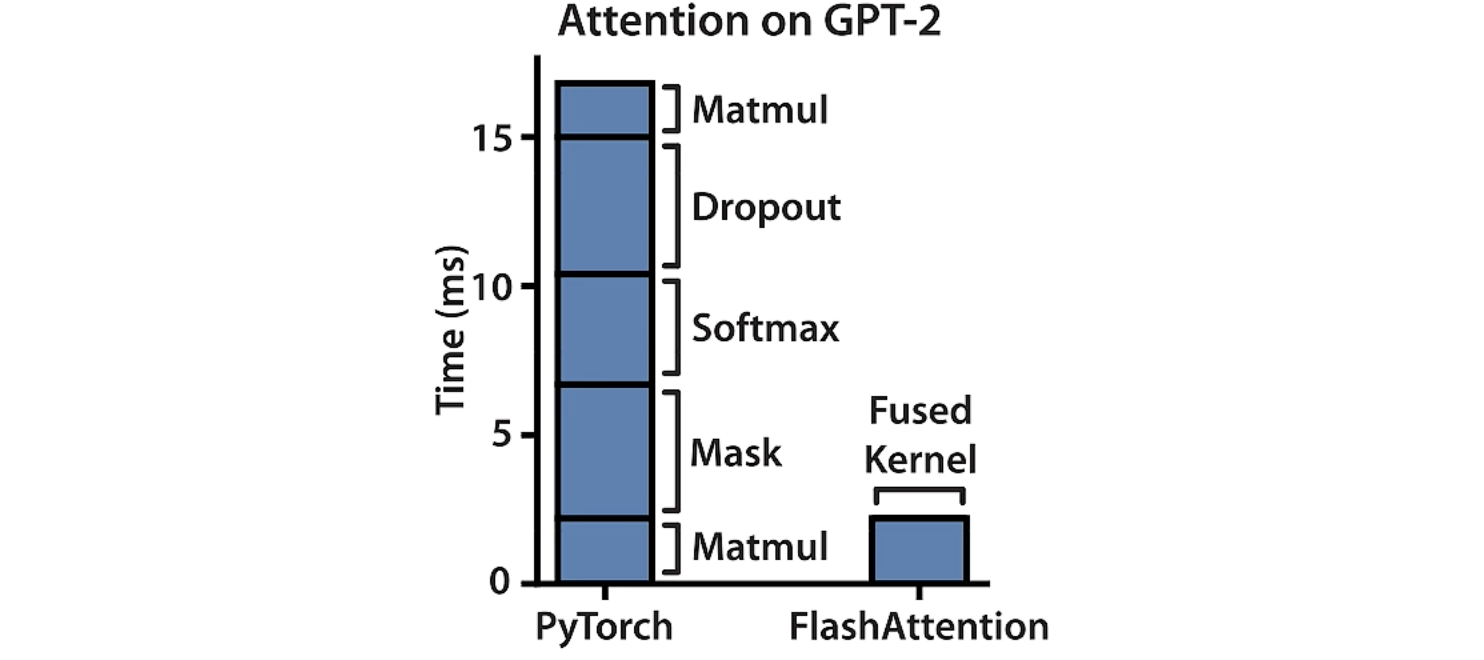
PyTorch 实现：

Matmul：计算 $S = Q K^{T}$ 或 $O = P V$ ，Compute-Bound（大规模矩阵乘法，主要消耗算力）
Mask：对注意力矩阵 $S$ 进行掩码（如因果遮盖）， Memory-Bound（元素级逻辑运算）
Softmax：计算注意力权重归一化 $P = softmax (S)$ ，Memory-Bound（涉及指数与规约求和操作）
Dropout：随机丢弃部分注意力权重，属于 Memory-Bound 操作（按位随机置零操作）
Matmul（第二次）：计算 $O = P V$ ，Compute-Bound（第二个大规模矩阵乘法）

FlashAttention 实现：

使用单个 Fused Kernel，在 SRAM 内完成以上所有步骤。
[*] 结果：
FlashAttention 的总耗时约为 PyTorch 的 1/3；
性能提升主要来源于减少了 HBM 访问次数，而非减少 FLOPs。

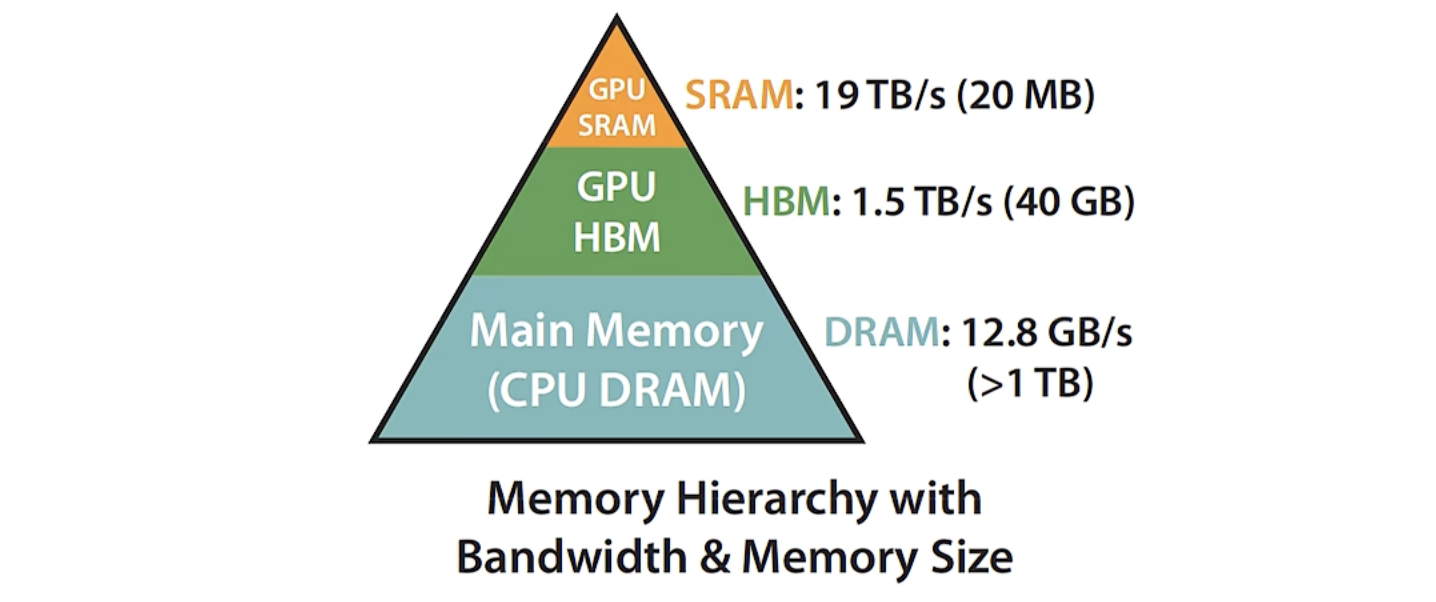
优化目标

避免 Attention Matrix 从 HBM 的频繁读写。 在传统实现中，注意力矩阵 $S = Q K^{T}$ 与 $P = softmax (S)$ 都需要写入并多次从 HBM 读取，造成严重的 IO 开销。
FlashAttention 的设计目标是在 保持精确计算结果 的前提下，彻底减少这些读写。

主要方法

分块计算（Tiling）与融合操作（Fusion）
将序列分为多个小块（tiles），在片上 SRAM 内完成：
- 计算 $S = Q K^{T}$
- 归一化 $P = softmax (S)$
- 计算 $O = P V$
  这些步骤被融合为一个 kernel，减少中间结果回写 HBM 的次数。
反向传播阶段的重计算（Recomputation）
在反向传播时，不再从显存中读取 $S$ 或 $P$ ，而是利用前向阶段保留的统计量（如 $max (S)$ 与归一化因子），在 SRAM 中重新计算必要的中间结果。通过以上策略，FlashAttention 既保持精确性，又显著降低 IO 成本。

性能效果

论文实验结果表明，在 A100 GPU 上：

速度提升：2–4 倍（随着序列长度增加而提升）
显存占用降低：10–20 倍

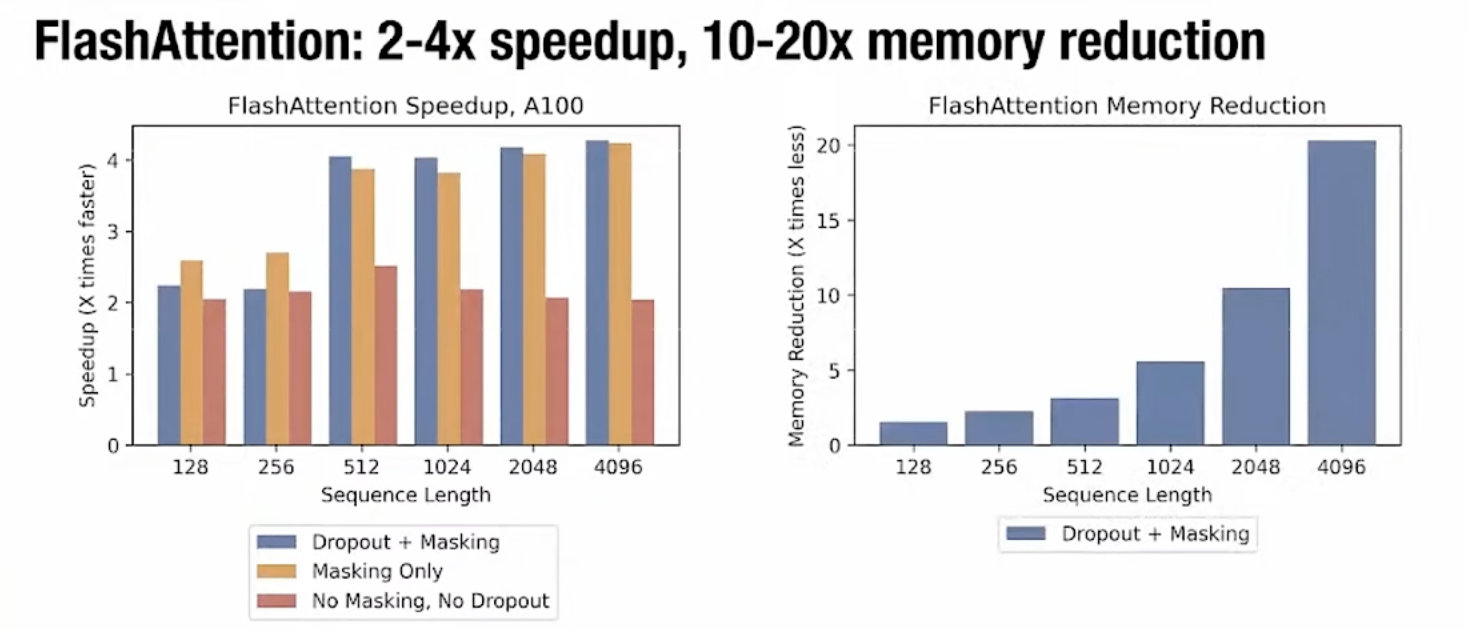
Speedup 对比（左图）

随着序列长度从 128 → 4096：

所有设置（含 Mask、Dropout 与否）均有约 2–4× 加速；
长序列下加速效果更明显；
FlashAttention 在相同 FLOPs 下大幅减少 HBM 访问。

Memory Reduction 对比（右图）

原显存占用随序列长度增长呈平方提升，而 FlashAttention 显存占用近似线性增长：

当序列长度为 4096 时，显存使用量下降约 20×；
因此可在同等硬件条件下支持更长上下文或更大模型。

前向传播算法流程与伪代码解析

Algorithm 1：FlashAttention

输入与内存设定

输入矩阵： $Q, K, V \in R^{N \times d}$ 存储在显存（HBM）中
片上缓存（SRAM）容量： $M$

步骤伪代码

Require: Matrices Q, K, V ∈ ℝ^(N×d) in HBM, on-chip SRAM of size M.
1. Set block sizes
    B_c = ⌈ M / (4d) ⌉,
    B_r = min(⌈ M / (4d) ⌉, d)
2. Initialize
    O = 0_(N×d), ℓ = 0_(N), m = -∞_(N)  (stored in HBM)
3. Divide Q, K, V into blocks:
    Q → {Q₁,…,Q_Tᵣ}, each size (B_r×d)
    K, V → {K₁,…,K_Tc}, each size (B_c×d)
4. Divide O, ℓ, m into matching row-blocks {Oᵢ}, {ℓᵢ}, {mᵢ}  
5. For j = 1 … T_c:                  # 外层循环：遍历列块 (K, V)  
6. Load K_j, V_j from HBM → SRAM   
7. For i = 1 … T_r:              # 内层循环：遍历行块 (Q)
8. Load Q_i, O_i, ℓ_i, m_i → SRAM
9. Compute S_ij = Q_i K_jᵀ            # 局部注意力得分
10. Compute m̃_ij = rowmax(S_ij)
    P̃_ij = exp(S_ij - m̃_ij)
    ℓ̃_ij = rowsum(P̃_ij)
11. Compute new scaling
    mᵢ^new = max(mᵢ, m̃_ij)
    ℓᵢ^new = e^(mᵢ - mᵢ^new) ℓᵢ + e^(m̃_ij - mᵢ^new) ℓ̃_ij
12. Update output block
   Oᵢ ← diag(ℓᵢ^new)⁻¹ [ diag(ℓᵢ) e^(mᵢ - mᵢ^new) Oᵢ + e^(m̃_ij - mᵢ^new) P̃_ij V_j ]
13. Write Oᵢ, ℓᵢ^new, mᵢ^new → HBM
14. End for
15. End for
16. Return O

步骤详解

1. 块划分（Tiling）
将长序列 $N$ 按行和列划分为若干小块：

行块（Row block）大小为 $B_{r}$
列块（Column block）大小为 $B_{c}$ 这样可以保证每个块 $Q_{i}, K_{j}, V_{j}$ 可以完全装入 SRAM。

2. 外层循环（第 5–6 行）
遍历每个列块 $(K_{j}, V_{j})$ ，一次性加载到 SRAM。

3. 内层循环（第 7–8 行）
遍历每个行块 $(Q_{i}, O_{i}, ℓ_{i}, m_{i})$ ，计算与当前列块的注意力结果。

4. 局部注意力计算（第 9–10 行）
在 SRAM 内计算局部得分矩阵：

$S_{i j} = Q_{i} K_{j}^{T}$
对每一行求最大值 $m ̃_{i j}$ ，用于数值稳定的 softmax
计算 $P ̃_{i j} = \exp (S_{i j} - m ̃_{i j})$
求局部归一化因子 $ℓ ̃_{i j} = \sum_{j} P ̃_{i j}$

5. 可加式 softmax 合并（第 11 行）
合并当前块与历史块的 softmax 统计：

$m_{i}^{n e w} = max (m_{i}, m ̃_{i j})$
$ℓ_{i}^{n e w} = e^{m_{i} - m_{i}^{n e w}} ℓ_{i} + e^{m ̃_{i j} - m_{i}^{n e w}} ℓ ̃_{i j}$
这一步确保跨块计算的数值等价于完整 softmax。

6. 输出更新（第 12 行）
更新输出块 $O_{i}$ ：

O_{i} = \frac{e^{m_{i} - m_{i}^{n e w}} ℓ_{i} O_{i} + e^{m ̃_{i j} - m_{i}^{n e w}} P ̃_{i j} V_{j}}{ℓ_{i}^{n e w}}

只需在 SRAM 中保存当前块的结果，然后写回 HBM。

7. 重复上述过程直至遍历所有块
最终输出 $O = softmax (Q K^{T}) V$ ，且无需物化完整的 $N \times N$ 注意力矩阵。

算法核心思想总结

将注意力计算拆分为小块，在片上缓存中完成局部运算；
使用可加式 softmax 统计 $(m, ℓ)$ ，保证结果与完整 softmax 等价；
不存储中间矩阵 $S, P$ ，只保存必要统计量；
实现了精确注意力的同时，大幅减少 HBM 读写。

反向传播的优化机制

反向传播的核心思路

在前向计算中，不保存完整的注意力矩阵 $S$ 或 $P$ ，而仅保留 softmax 的统计值：

每一行的最大值 $m_{i} = max_{j} S_{i j}$
每一行的累积和（归一化因子） $ℓ_{i} = \sum_{j} \exp (S_{i j} - m_{i})$

这两个值相当于 softmax 的“梯度检查点”，允许反向传播阶段快速重建激活值（softmax 输出），而无需从 HBM 重新读取中间矩阵。换句话说，FlashAttention 的反向传播采用了一种 “以计算换显存（recompute instead of store）” 的策略。

反向传播的实现要点

前向阶段
- 保存 $(m_{i}, ℓ_{i})$ 两个统计量；
- 不保存 $S$ 或 $P$ 。
反向阶段
- 重新根据 $Q_{i}, K_{j}, m_{i}, ℓ_{i}$ 局部重计算： $P_{i j} = \frac{\exp (S_{i j} - m_{i})}{ℓ_{i}}$
- 使用该 $P_{i j}$ 来计算梯度： $d Q = d O V^{T} P, d K = P^{T} (d O Q), d V = P^{T} d O$
由于只需重算局部块的 $S_{i j}$ ，且 $Q_{i}, K_{j}$ 可从 HBM 顺序加载，整体 IO 成本极低。

这种方法的代价是 FLOPs 稍有增加（重算一次 $S_{i j}$ ），但由于极大减少了 HBM 读写，整体仍显著提速。

性能对比（反向传播阶段）

Attention	GFLOPs	HBM R/W (GB)	Runtime (ms)
Standard	66.6	40.3	41.7
FlashAttention	75.2	4.4	7.3

对比说明：

FlashAttention 的计算量（GFLOPs）略高（重算造成的开销）；
显存读写量下降近 10 倍；
实际运行时间缩短至原来的 1/6。

直观理解

可以把 $(m_{i}, ℓ_{i})$ 看作 softmax 的压缩状态（activation checkpoint）：

它记录了每行 softmax 的数值范围与归一化比例；
反向传播时通过这些值可以“还原”出 softmax 激活；
因此既保留了正确的梯度传播，又显著降低了内存消耗。

FLashAttention - 2

减少非矩阵乘法计算

FlashAttention-2 进一步将注意力过程中的所有主要操作（包括 QKᵀ 与 PV）统一到标准的矩阵乘法（GEMM）形式中。

这样可以完全利用 GPU 的 Tensor Core 进行加速，避免了前一版本中部分按元素操作（element-wise op）的低效执行。

调整计算循环顺序（内外层训练循环）

FlashAttention-2 重新组织计算流程：

Q 块作为外层循环；
K、V 块作为内层循环；这样做可以让每个 Q 块在一次加载后重用多个 KV 块，显著减少 HBM（显存）与 SRAM（片上缓存）之间的读写次数。

跳过上三角无效计算（Causal Mask 优化）

对于自回归模型（如 GPT 类），注意力矩阵的上三角区域是被掩码的（即未来时刻不可见）。

FlashAttention-2 在块级别上检测：

若当前计算块完全位于上三角（被 Mask 区域），则直接跳过计算；
仅对矩阵的下三角与对角区域执行 attention。

这减少了冗余的矩阵乘法与 softmax 操作，提高了整体效率。

FlashAttention：Attention加速 ​

原始 Attention 的实现方式 ​

存储关系 ​

原始 Attention 的计算流程 ​

关键问题：显存与访存瓶颈 ​

实际例子 ​

小结 ​

Compute-Bound 与 Memory-Bound ​

Compute-Bound 运算 ​

Memory-Bound 运算 ​

Memory-Bound 的优化思路 ​

核心优化思路与性能提升 ​

性能对比示意（以 GPT-2 为例） ​

优化目标 ​

主要方法 ​

性能效果 ​

Speedup 对比（左图） ​

Memory Reduction 对比（右图） ​

前向传播算法流程与伪代码解析 ​

Algorithm 1：FlashAttention ​

输入与内存设定 ​

步骤伪代码 ​

步骤详解 ​

算法核心思想总结 ​

反向传播的优化机制 ​

反向传播的核心思路 ​

反向传播的实现要点 ​

性能对比（反向传播阶段） ​

直观理解 ​

FLashAttention - 2 ​